Threads Matrixmultiplikation parallel

[Ion]

Es geht derzeit bei uns um parallele Verarbeitung und jetzt sollen wir eine parallele Implementierung von 2 Algorithmen einmal praktisch umsetzen. Ich komme aber wohl anscheinend mit dem angegebenen Algorithmus klar. Der eine verwendet dann nämlich die transponierte Matrix von b und die Berechnung sieht so aus:

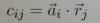
Das dann noch so in zwei Schleifen eingepackt, wovon die in dem Bild oben parallelisiert werden soll.

for(i = 0; i < rowsMatA; i++) {
   final int iFin = i;

  threadPoolExec.execute(new Runnable() {
  @Override
  public void run() {
       for(int j = 0; j < colsMatB; j++) {
         c[iFin][j] = matA.data[iFin][0] * r.data[0][j];
       }
  }
  });
}

Ich habe für die Matrix extra eine eigene Klasse geschrieben und bei dem Member data handelt es sich um das Arrray das die Matrix hält. Der "threadPoolExec" ist ein ThreadPoolExecutor aus dem java.util.concurrent Package und wofür rowsMatA und wofür colsMatB steht sollte ja klar sein.

Leider kriege ich aber mit der obigen Implementierung (falls meine richtig ist, was wohl nicht der Fall ist ... ) immer das falsche Ergebnis raus. Ich habe das ganze auch einmal in "normal" implementiert, also mit 3 Schleifen und dann die innerste parallel, auch mit dem ThreadPoolExecutor als Hilfsmittel und da kriege ich das richtige Ergebnis raus. Die Ergebnisse sollten ja identisch sein?

Wenn ich die Matrizen habe (Darstellung als 2D Array in Java)

{{2,4},{6, 8}});
{{4,6},{8,10}});

dann sollte doch

{{40,52},{88,116}});

dabei rauskommen, oder nicht?

Ich kriege aber mit der obigen Implementierung

{{0,16},{24,48}});

herraus.

Mit dem normalen Alg. kriege ich das, wie gesagt heraus und ebenfalls dasselbe auch per Hand und online. Was mache ich also falsch? Mich wundert das aber auch ehrlich gesagt, dass das wohl mit 2 Schleifen laufen soll? Geht das überhaupt?

Ich habe, wie schon gesagt die Matrix B vorher transponiert aber kann man das mit nur 2 Schleifen dann nachher überhaupt berechnen? Die Variante habe ich jedenfalls so vorher noch nie verwendet und auch gesehen.

Die zweite Variante soll so aussehen:

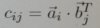
Dabei wird dann die äußere Schleife parallelisiert. Da wird dann wohl mit dem transponierten Spaltenvektor gerechnet aber da habe ich mich noch nicht rangemacht. Da frage ich mich allerdings auch wieder, ob das überhaupt mit 2 Schleifen geht? Müsste man da nicht auch nohh erst den Spaltenvektor transponieren, also noch einmal 2 Schleifen dazu? Bei dem anderen steht vorher noch explizit davor, dass r = b^T sein soll, also die transponierte Matrix von B.

Wir sollen auch noch eine Aussage zur Laufzeit der beiden Algorithmen machen und sagen, welcher von beiden dann wohl besser sein soll und auch im Vergleich zum "normalen" Algortihmus, wo man dann einfach 3 Schleifen hat, also so:

for(i = 0; i < rowsMatA; i++) {
   for(j = 0; j < colsMatB; j++) {
     for(k = 0; k < rowsMatB; k++) {
       c[i][j] += matA.data[i][k] * matB.data[k][j];
     }
   }
}

Wenn das wirklich mit 2 Schleifen bei der Berechnung funktioniert, dann müsste der erste doch der beste sein oder nicht? Da hätte man dann ja nicht mehr eine Laufzeit von n^3, wobei n die Anzahl der Zeilen und Spalten ist. Bei dem zweiten hätte man ja (meiner Meinung nach) ja noch 2 zusätzliche Schleifen, was ja auf jeden Fall schlechter ist als der erste und auch schlechter als der "normale". Liege ich damit richtig?

c ist dabei ein 2D-Array, woraus ich nachher ebenfalls dann ein Matrix Objekt erzeuge und matA und matB sind schon Matrix Objekte, weswegen ich da ja ein matA.data stehen habe, da es sich dabei um das 2D-Array des Matrix Objektes handelt. Nur noch einmal zur Klarstellung.

 

[Nuiton]

Ja, es gibt eine offesichtliche O(N^3) Loesung sowohl als auch eine O(N^2) Loesung.
Ja, O(N^2) ist besser als O(N^3). Oder was spricht dagegen?
Ja, ich bekomme das gleiche Resultat, wenn ich die beiden Matrizen multipliziere, bzw.

40    52  
88    116

 

[Ion]

Ja, dass es solche Lösungen gibt ist mir schon klar aber haben die beiden dann wirklich eine Rechenlaufzeit von O(N^2)? Ich kriege ja, wie gesagt nicht das richtige Ergebnis heraus. Ich kriege

{{0,16},{24,48}});

heraus, anstatt von

{{40,52},{88,116}});

Eine Laufzeit bei einer Matrixmultiplikation von O(N^2) ist ja schon verdammt gut und ich dachte jetzt nicht, dass man es mit so einem naiven Algorithmus zu einer Laufzeit von O(N^2) bringen würde. Das sind doch dann eher die wirklich ausgeklügelten Algortithmen, oder nicht?´

Das O(N^2) besser ist als O(N^3) habe ich ja nicht gefragt, sondern ob die beiden oben genannten Algorithmen eine Laufzeit von O(N^2) haben, wobei das ja dann nur die reine Rechenzeit wäre, weil man ja vorher bei dem ersten Algorithmus ja noch die Matrix B transponieren müsste, was ja insgesamt zu O(N^2) + O(N^2) führen sollte?

Meine Frage ist, falls das oben nicht richtig rausgekommen ist, ob ich drei Schleifen bei der Berechnung brauche, oder ob das so schon reicht und ich da irgendwas (und wenn ja), was falsch habe und auch noch die Frage zur Laufzeit. Der erste Algorithmus mit der transponierten Matrix ist doch besser als der zweite mit dem transponierten Spaltenvektor, oder? Zumal bei dem ersten ja auch noch die Berechnung parallelisiert wird und bei dem zweiten nur die erste Schleife.

Ich muss mich wohl dafür entschuldigen, dass ich das oben so ein wenig komisch formuliert habe aber es war schon spät und ich war extrem aufgekratzt.

 

[Nuiton]

was ja insgesamt zu O(N^2) + O(N^2) führen sollte

O(N^2) + O(N^2) = O(max(O(N^2), O(N^2)) = O(N^2) (siehe ein Buch zum Thema Funktionsanalysis).

Falsch:

for(i =0; i < rowsMatA; i++){
   for(j =0; j < colsMatB; j++){
     for(k =0; k < rowsMatB; k++){
       c[i][j]+= matA.data[i][k]* matB.data[k][j];
     }
   }
}

Richtig:

for(i =0; i < rowsMatA; i++){
   for(j =0; j < colsMatB; j++){
     for(k =0; k < colsMatA; k++){
       c[i][j]+= matA.data[i][k]* matB.data[k][j];
     }
   }
}

Unterschied:

     for(k =0; k < colsMatA; k++){
       c[i][j]+= matA.data[i][k]* matB.data[k][j];
     }

 

[Ion]

O(N^2) + O(N^2) = O(max(O(N^2), O(N^2)) = O(N^2) (siehe ein Buch zum Thema Funktionsanalysis).

Jo, ich habe ja auch gesagt eine reine Rechenzeit von O(N^2).

Zur Multiplikation:
Hm .. stimmt schon. Da müsste schon bei der normalen Multiplikation mit der Laufzeit von O(N^3) ein columnsMatA stehen, obwohl das ja eigentlich egal ist? Die Multiplikation ist aber auch eigentlich nicht das Problem. Es geht da ja um diese hier; mit der transponierten Matrix von B:

for(i = 0; i < rowsMatA; i++) {
   final int iFin = i;

  threadPoolExec.execute(new Runnable() {
  @Override
  public void run() {
       for(int j = 0; j < colsMatB; j++) {
         c[iFin][j] = matA.data[iFin][0] * r.data[0][j];
       }
  }
  });
}

Hier einmal der Pseudo-Code dieser Matrixmultiplikation:


Die liefert mir ja das falsche Ergebnis, egal was ich da reingebe. Die andere, die ich oben angegeben habe, rechnet ja auch richtig. Ob ich colsMatA oder rowsMatB schreibe ist doch egal?

 

[JStein52]

Muss nicht colsMatA == rowsMatB sein und deshalb beides richtig ?

 

[mrBrown]

Hier einmal der Pseudo-Code dieser Matrixmultiplikation:

Wenn ich mich grad nicht vertue sind a_j und r_i Vekoren und das ganze eine Skalarmultiplikation, deren Laufzeit wäre O(N) mit N Länge der Vektoren, das ganze also wieder in O(N^3).
Da liegt auch der Fehler in deinem Algo, du nimmst jeweils nur die ersten Werte der beiden Vektoren, anstatt aller Werte

Das Transponieren kann man ignorieren, und stattdessen innerhalb der Rechnung mit vertauschten Indizes arbeiten.