intersect von zwei Rechtecken

[Schuriko]

Ich suche gerade zwei effiziente Methoden, die

1. bestimmen ob sich zwei Rechtecke überschneiden
2. den Bereich (als Rechteck) der Überschneidung

 

[mihe7]

Was gefällt Dir an den betreffenden Methoden von java.awt.Rectangle bzw. java.awt.geom.Rectangle2D nicht?

 

[Schuriko]

Was gefällt Dir an den betreffenden Methoden von java.awt.Rectangle bzw. java.awt.geom.Rectangle2D nicht?

Das war nicht die Frage

 

[kneitzel]

??? Du suchst effektive Methoden und du wurdest auf Methoden hingewiesen. Hast Du Dir diese mal angesehen?

Oder was stört Dich an den Methoden?

 

[httpdigest]

Wenn du ein Rechteck durch den minimalen und maximalen Eckpunkt beschreibst, dann:

public boolean intersects(Rectangle other) {
    return minX < other.maxX && maxX >= other.minX &&
           maxY >= other.minY && minY < other.maxY;
}
public Rectangle intersect(Rectangle other) {
    float nMinX = Math.max(minX, other.minX), nMinY = Math.max(minY, other.minY);
    float nMaxX = Math.min(maxX, other.maxX), nMaxY = Math.min(maxY, other.maxY);
    if (nMinX > nMaxX || nMinY > nMaxY) {
        return null;
    }
    return new Rectangle(nMinX, nMinY, nMaxX, nMaxY);
}

 

[Schuriko]

??? Du suchst effektive Methoden und du wurdest auf Methoden hingewiesen. Hast Du Dir diese mal angesehen?

Oder was stört Dich an den Methoden?

Weil mich der Algo interessiert und dieses sieht man nun mal nicht bei einer closed function

 

[Schuriko]

Wenn du ein Rechteck durch den minimalen und maximalen Eckpunkt beschreibst, dann:

public boolean intersects(Rectangle other) {
    return minX < other.maxX && maxX >= other.minX &&
           maxY >= other.minY && minY < other.maxY;
}
public Rectangle intersect(Rectangle other) {
    float nMinX = Math.max(minX, other.minX), nMinY = Math.max(minY, other.minY);
    float nMaxX = Math.min(maxX, other.maxX), nMaxY = Math.min(maxY, other.maxY);
    if (nMinX > nMaxX || nMinY > nMaxY) {
        return null;
    }
    return new Rectangle(nMinX, nMinY, nMaxX, nMaxY);
}

Danke dir! Jetzt weis ich wie man es am effektivsten erfüllen kann.

 

[temi]

Weil mich der Algo interessiert und dieses sieht man nun mal nicht bei einer closed function

Von Algorithmus kann man da kaum sprechen, es werden einfach nur ein paar Vergleiche gemacht und bezüglich "closed function":

http://developer.classpath.org/doc/java/awt/Rectangle-source.html

 

[kneitzel]

Jo, der Source kann ja eingesehen werden. Daher kann das JDK sehr gut als Referenz genommen werden.

 

[OpaTom]

Wenn du ein Rechteck durch den minimalen und maximalen Eckpunkt beschreibst, dann:

public boolean intersects(Rectangle other) {
    return minX < other.maxX && maxX >= other.minX &&
           maxY >= other.minY && minY < other.maxY;
}
public Rectangle intersect(Rectangle other) {
    float nMinX = Math.max(minX, other.minX), nMinY = Math.max(minY, other.minY);
    float nMaxX = Math.min(maxX, other.maxX), nMaxY = Math.min(maxY, other.maxY);
    if (nMinX > nMaxX || nMinY > nMaxY) {
        return null;
    }
    return new Rectangle(nMinX, nMinY, nMaxX, nMaxY);
}

So allgemein, wie die Frage gestellt ist, ist das eine falsche Antwort. Die Rechtecke könnten in der Ebene unterschiedlich gedreht sein. Wenn die Projektionen auf die X/Y Achsen sich überschneiden, könnte es doch sein, dass die Rechtecke in der Ebene sich nicht berühren, sondern nebeneinander liegen.. Damit die Antwort korrekt wäre, müsste eines der Rechtecke zwei Seiten parallel zum Koordinatensystem haben.

 

[White_Fox]

Gaaaaanz genau, und es war ja auch nie die Rede von einem kartesischem Koordinatensysten, kann ja auch ein radiales sein.

Mal im Ernst: Schuriko ist seit Ende 2021 nicht mehr hier gewesen, ob ihn das noch interessiert? Wie gräbt man immer so alte Themen aus?

 

[bärrr]

Prinzipiell hat @OpaTom recht, die Intersecting-Berechnung ist nicht ganz so einfach, wie von @httpdigest beschrieben, wenn die Rechtecke auch "schief" sein können:

import javax.swing.*;
import java.awt.*;
import java.util.Timer;
import java.util.TimerTask;

public class Box2D {
    private double[][] box1 = {
            {1, 1},
            {1, 2},
            {2, 2},
            {2, 1}
    };
    private double[][] box2 = {
            {1.85, 1.85},
            {1.85, 2.85},
            {2.85, 2.85},
            {2.85, 1.85}
    };

    private void drawBoxes(Graphics2D g2d) {
        if (isIntersecting()) {
            g2d.setColor(Color.RED);
        } else {
            g2d.setColor(Color.BLUE);
        }
        for (int i = 0; i < box1.length; i++) {
            int j = (i + 1) % box1.length;
            g2d.drawLine((int) (box1[i][0] * 100), (int) (box1[i][1] * 100), (int) (box1[j][0] * 100), (int) (box1[j][1] * 100));
        }
        for (int i = 0; i < box2.length; i++) {
            int j = (i + 1) % box2.length;
            g2d.drawLine((int) (box2[i][0] * 100), (int) (box2[i][1] * 100), (int) (box2[j][0] * 100), (int) (box2[j][1] * 100));
        }
    }

    private void rotateBoxAtCenter(double[][] box, double degrees) {
        double centerX = 0;
        double centerY = 0;
        for (double[] point : box) {
            centerX += point[0];
            centerY += point[1];
        }
        centerX /= box.length;
        centerY /= box.length;
        for (double[] point : box) {
            double x = point[0] - centerX;
            double y = point[1] - centerY;
            point[0] = x * Math.cos(Math.toRadians(degrees)) - y * Math.sin(Math.toRadians(degrees)) + centerX;
            point[1] = x * Math.sin(Math.toRadians(degrees)) + y * Math.cos(Math.toRadians(degrees)) + centerY;
        }
    }

    private boolean isIntersecting() {
        for (int i = 0; i < box1.length; i++) {
            int j = (i + 1) % box1.length;
            for (int k = 0; k < box2.length; k++) {
                int l = (k + 1) % box2.length;
                if (doIntersect(box1[i][0], box1[i][1], box1[j][0], box1[j][1], box2[k][0], box2[k][1], box2[l][0], box2[l][1])) {
                    return true;
                }
            }
        }
        return false;
    }

    private boolean doIntersect(double v, double v1, double v2, double v3, double v4, double v5, double v6, double v7) {
        double a1 = v3 - v1;
        double b1 = v - v2;
        double c1 = a1 * (v) + b1 * (v1);
        double a2 = v7 - v5;
        double b2 = v4 - v6;
        double c2 = a2 * (v4) + b2 * (v5);
        double determinant = a1 * b2 - a2 * b1;
        if (determinant == 0) {
            return false;
        }
        double x = (b2 * c1 - b1 * c2) / determinant;
        double y = (a1 * c2 - a2 * c1) / determinant;
        return x >= Math.min(v, v2) && x <= Math.max(v, v2) && y >= Math.min(v1, v3) && y <= Math.max(v1, v3) && x >= Math.min(v4, v6) && x <= Math.max(v4, v6) && y >= Math.min(v5, v7) && y <= Math.max(v5, v7);
    }

    public Box2D() {
        JFrame frame = new JFrame("Box2D");
        frame.setDefaultCloseOperation(JFrame.EXIT_ON_CLOSE);
        frame.setSize(400, 400);
        frame.add(new JPanel() {
            @Override
            protected void paintComponent(Graphics g) {
                super.paintComponent(g);
                drawBoxes((Graphics2D) g);
            }
        });
        frame.setVisible(true);

        new Timer().scheduleAtFixedRate(new TimerTask() {
            @Override
            public void run() {
                rotateBoxAtCenter(box1, 1);
                rotateBoxAtCenter(box2, 2);
                frame.repaint();
            }
        }, 1000 * 10, 25);
    }

    public static void main(String[] args) {
        Box2D box2D = new Box2D();
    }
}

 

[bärrr]

Edit: Bei Kreisen würde man über die Entfernung der Mittelpunkte gehen, aber bei Rechtecken ist das natürlich nicht ganz so einfach (ein Rechteck ist ja schließlich kein Kreis ... )

Bei mehreren Kreisen würde man einen Weg abklappern: https://csaws.cs.technion.ac.il/~itai/publications/Algorithms/min-circuit.pdf

Und bei irgendwelchen anderen Gebilden (n-Polygonen) bleibt schließlich nur noch flood fill übrig (als effizientes Verfahren).

 

[mihe7]

Und bei irgendwelchen anderen Gebilden (n-Polygonen) bleibt schließlich nur noch flood fill übrig (als effizientes Verfahren).

Sofern die Polygone konvex sind, geht's z. B. auch mit dem Trennungssatz.

 

[bärrr]

Sofern die Polygone konvex sind

Ja, da war ja was. Aber man müsste erst mal bestimmen, ob ein gegebenes ("wildes") Polygon konvex oder konkav ist, indem man die Kanten abgeht ... (das dauert ja auch etwas)

Ich habe noch mal schnell ein Refactoring gemacht:

import javax.swing.*;
import java.awt.*;
import java.util.Timer;
import java.util.TimerTask;

public class Box2D {
    private double[][] box1 = {
            {1, 1},
            {1, 2},
            {2, 2},
            {2, 1}
    };
    private double[][] box2 = {
            {1.85, 1.85},
            {1.85, 2.85},
            {2.85, 2.85},
            {2.85, 1.85}
    };

    private void drawBoxes(Graphics2D g2d) {
        if (isIntersecting()) {
            g2d.setColor(Color.RED);
        } else {
            g2d.setColor(Color.BLUE);
        }
        for (int i = 0; i < box1.length; i++) {
            int j = (i + 1) % box1.length;
            g2d.drawLine((int) (box1[i][0] * 100), (int) (box1[i][1] * 100), (int) (box1[j][0] * 100), (int) (box1[j][1] * 100));
        }
        for (int i = 0; i < box2.length; i++) {
            int j = (i + 1) % box2.length;
            g2d.drawLine((int) (box2[i][0] * 100), (int) (box2[i][1] * 100), (int) (box2[j][0] * 100), (int) (box2[j][1] * 100));
        }
    }

    private void rotateBoxAtCenter(double[][] box, double degrees) {
        double centerX = 0;
        double centerY = 0;
        for (double[] point : box) {
            centerX += point[0];
            centerY += point[1];
        }
        centerX /= box.length;
        centerY /= box.length;
        double radians = Math.toRadians(degrees);
        for (double[] point : box) {
            double x = point[0] - centerX;
            double y = point[1] - centerY;
            point[0] = x * Math.cos(radians) - y * Math.sin(radians) + centerX;
            point[1] = x * Math.sin(radians) + y * Math.cos(radians) + centerY;
        }
    }

    private boolean isIntersecting() {
        for (int i = 0; i < box1.length; i++) {
            int j = (i + 1) % box1.length;
            for (int k = 0; k < box2.length; k++) {
                int l = (k + 1) % box2.length;
                if (doIntersect(box1[i][0], box1[i][1], box1[j][0], box1[j][1], box2[k][0], box2[k][1], box2[l][0], box2[l][1])) {
                    return true;
                }
            }
        }
        return false;
    }

    private boolean doIntersect(double v, double v1, double v2, double v3, double v4, double v5, double v6, double v7) {
        double a1 = v3 - v1;
        double b1 = v - v2;
        double c1 = a1 * v + b1 * v1;
        double a2 = v7 - v5;
        double b2 = v4 - v6;
        double c2 = a2 * v4 + b2 * v5;
        double determinant = a1 * b2 - a2 * b1;
        if (determinant == 0) {
            return false;
        }
        double x = (b2 * c1 - b1 * c2) / determinant;
        double y = (a1 * c2 - a2 * c1) / determinant;
        return x >= Math.min(v, v2) && x <= Math.max(v, v2) && y >= Math.min(v1, v3) && y <= Math.max(v1, v3) && x >= Math.min(v4, v6) && x <= Math.max(v4, v6) && y >= Math.min(v5, v7) && y <= Math.max(v5, v7);
    }

    public Box2D() {
        JFrame frame = new JFrame("Box2D");
        frame.setDefaultCloseOperation(JFrame.EXIT_ON_CLOSE);
        frame.setSize(400, 400);
        frame.add(new JPanel() {
            @Override
            protected void paintComponent(Graphics g) {
                super.paintComponent(g);
                drawBoxes((Graphics2D) g);
            }
        });
        frame.setVisible(true);

        new Timer().scheduleAtFixedRate(new TimerTask() {
            @Override
            public void run() {
                rotateBoxAtCenter(box1, -0.5);
                rotateBoxAtCenter(box2, 1);
                frame.repaint();
            }
        }, 1000 * 10, 25);
    }

    public static void main(String[] args) {
        Box2D box2D = new Box2D();
    }
}

• in rotateBoxAtCenter fehlte was (double radians Variable)
• doIntersect enthielt unnötige Klammern
• und im TimerTask führt -0.5 und 1 zu einer "glatteren" Animation

... Hier vielleicht nicht notwendig, aber vielleicht sollte man auch den EDT verwenden?

Btw ... ich hatte die 1.85 und 2.85 willkürlich gewählt, aber vermutlich wäre 1+(pi/4) und 2+(pi/4) für die Koords sinnvoller ...

 

[bärrr]

ich hatte die 1.85 und 2.85 willkürlich gewählt, aber vermutlich wäre 1+(pi/4) und 2+(pi/4) für die Koords sinnvoller

@mihe7 es wäre ein Optimierungsproblem ... Wenn sich nur eine Box drehen würde, wäre es:

    private double[][] box2 = {
            {1 + Math.PI / 4 * 1.125, 1 + Math.PI / 4 * 1.125},
            {1 + Math.PI / 4 * 1.125, 2 + Math.PI / 4 * 1.125},
            {2 + Math.PI / 4 * 1.125, 2 + Math.PI / 4 * 1.125},
            {2 + Math.PI / 4 * 1.125, 1 + Math.PI / 4 * 1.125}
    };

Also müsste die zweite Box um ein Viertel Pi + ein Achtel verschoben sein (bin mir da aber nicht hundertprozentig sicher).



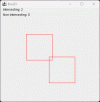
Wenn sich beide Boxen asynchron drehen würden (wie oben gezeigt), dann geht es vermutlich schon stark in die analytische Mathematik.

 

[thom4]

Ich suche gerade zwei effiziente Methoden, die

1. bestimmen ob sich zwei Rechtecke überschneiden
2. den Bereich (als Rechteck) der Überschneidung

Um zu überprüfen, ob sich zwei Rechtecke überschneiden, könntest du zunächst die Koordinaten der beiden Rechtecke (z. B. durch ihre Ecken) vergleichen. Wenn die Rechtecke sich nicht überlappen, gibt es einen einfachen Test, bei dem man sicherstellt, dass die rechte Seite des ersten Rechtecks nicht links von der linken Seite des zweiten Rechtecks liegt und umgekehrt. Dasselbe gilt für die obere und untere Seite der Rechtecke.

Für den Bereich der Überschneidung kannst du einfach die maximalen und minimalen Werte der Ecken der beiden Rechtecke ermitteln. Das bedeutet, dass du das „Überlappungs-Rechteck“ durch den maximalen linken und oberen Wert und den minimalen rechten und unteren Wert der beiden Rechtecke definierst. Wenn die Rechtecke sich tatsächlich überschneiden, ergibt sich daraus ein gültiges Rechteck.

Ein einfacher Algorithmus sieht ungefähr so aus: Wenn die Rechtecke sich überschneiden, berechne die Koordinaten des Überschneidungsbereichs durch den Maximalwert der linken und oberen Kanten und den Minimalwert der rechten und unteren Kanten. Wenn der Maximalwert größer ist als der Minimalwert, bedeutet das, dass es eine echte Überschneidung gibt.